始めに
半径 R の球状粒子からの散乱強度 I(q) は以下の式で表されます.この式からわかるように、球状粒子の散乱では、特定の q において I(q) = 0 となります.
I(q) = 9(qR)−6(sin qR − qR cos qR )2 (7.1)
ここで,I(q) を q に対して両対数でプロットすると,図 7.1 に示すように I(q) = 0 となるところが,特徴的な落ち込みとして強調されます.
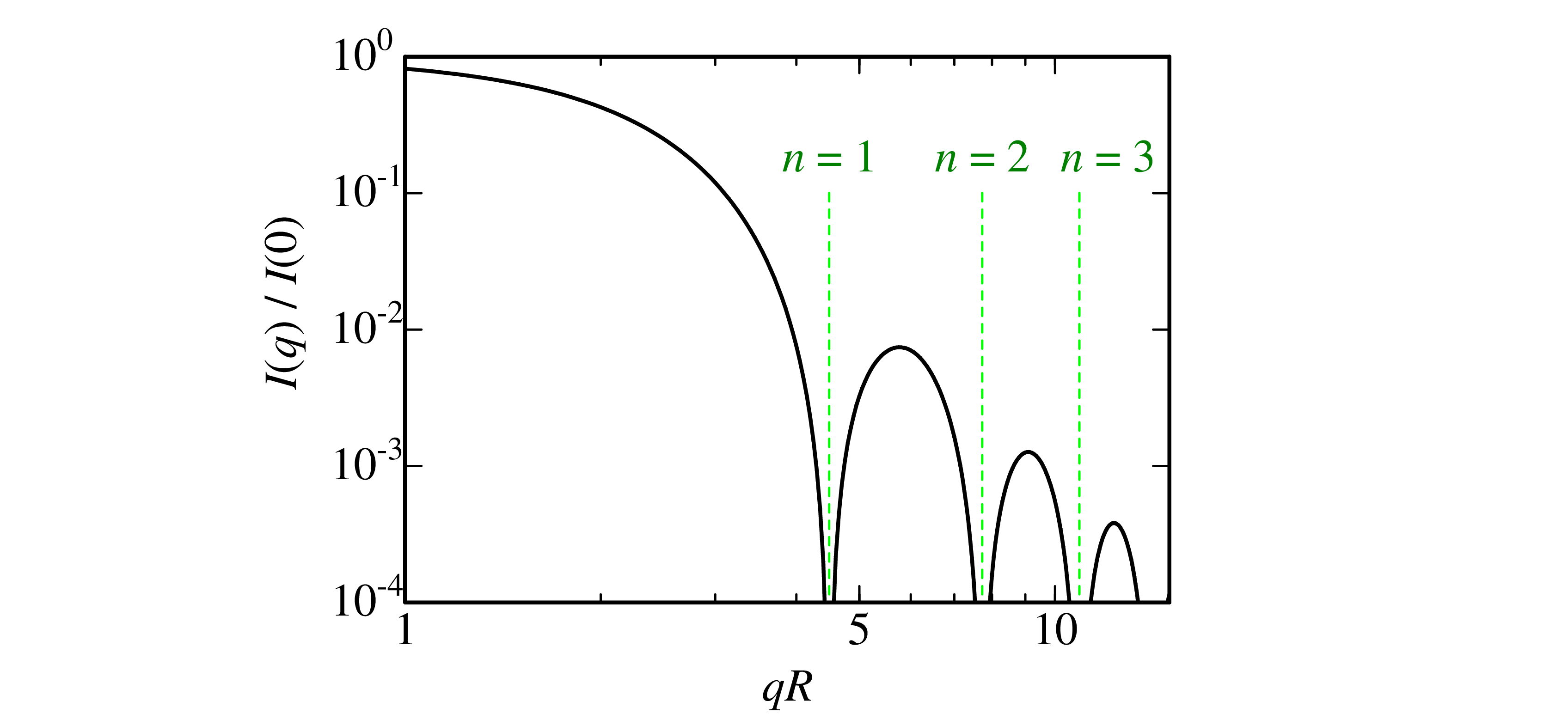
図7.1 球状粒子の散乱プロファイル
この落ち込み部分(しばしばフリンジと呼ばれます)を観測することで,定性的に球状粒子か判別することがしばしば行われるます.したがって,球状粒子を含む系の散乱実験においては,散乱プロファイル上にフリンジが含まれることが望ましいです.
フリンジの位置
球の半径が R である場合にフリンジが表れる q の位置を qf とすると,式(7.1)より
tan qfR = qfR (7.2)
の関係があることがわかります。この式を数値的に解くと,複数の解が得られます.その解をqの小さい方から順にqf,n (n = 1, 2, 3,...) とすると,
qf,n = 4.493, 7.725, 10.90,... (n = 1, 2, 3,...) (7.3)
となります.この計算尺では,式(7.3)で表される対応関係を n = 1, 2, 3 の場合について表示します.
対応関係の表示
対応関係を表示させる方法は次の通りです.下滑尺をドラッグして,∝1/q 尺上の R.sphere (fringe) と書かれた部分にある (1),(2),または (3) のいずれかの目盛りを,q 尺の 1 の目盛りに合わせます.R.sphere (fringe) の (1),(2),(3) の目盛りは,それぞれ,n = 1, 2, 3 の場合に対応しています.
これで,∝1/q 尺には球の半径 R が,q 尺にはフリンジ位置 qf が表示されています.カーソルを合わせて,対応関係を読み取ってください.